|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
2 Основы синтеза цифровых устройств 2.1 Последовательность операций при синтезе цифровых устройств комбинационного типа 1 Составление таблицы истинности комбинационного цифрового устройства (КЦУ) согласно его определения, назначения, словесного описания принципа работы. 2 Составление логической формулы согласно таблицы истинности. 3 Анализ полученной формулы с целью построения различных вариантов и нахождения наилучшего из них по тем или иным критериям. 4 Составление функциональной схемы КЦУ из элементов И, ИЛИ, НЕ. 2.2 Аналитическая запись логической формулы КЦУ Запись в форме СДНФ (Совершенная дизъюнктивная нормальная форма). В СДНФ логическая формула представляет собой логическую сумму нескольких логических произведений, в каждое из которых входят все независимые переменные с отрицанием или без него. Формула получается в два этапа: а) Записывается логическая сумма произведений, в каждое из которых входят все независимые переменные. Количество слагаемых равно числу наборов таблицы истинности, на которых логическая функция равна «1»; б) ставится знак инверсии над теми независимыми переменными, которые равны «0» в рассматриваемом наборе. Запись в форме СКНФ (Совершенная конъюнктивная нормальная форма). В СКНФ формула представляет собой логическое произведение нескольких логических сумм, в каждую из которых все независимые переменные с отрицанием или без него. Как и в предыдущем случае, формула получается в два этапа: а) Записывается логическое произведение всех сомножителей; количество сомножителей равно числу наборов таблицы истинности, на которых логическая функция равна «0»; б) ставится знак инверсии над теми независимыми переменными, которые равны «1» в рассматриваемом наборе. Структурные формулы в виде СДНФ и СКНФ эквивалентны и, с помощью законов алгебры, логики могут быть преобразованы одна в другую. Пример: Синтезировать мажоритарный логический элемент на три входа. Мажоритарным называется логический элемент, выходное состояние которого совпадает с большинством входных сигналов. На основании данного словесного описания мажоритарного элемента составлена его таблица истинности (Таблица 5). Таблица 5 - Таблица истинности мажоритарного элемента
На основе таблицы истинности записывается СДНФ или СКНФ функции, а затем составляется функциональная схема элемента. СДНФ: СКНФ: 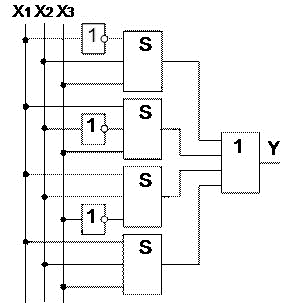 Рисунок 3 Функциональная схема мажоритарного элемента Функциональная схема элемента, составленная на основе функции СДНФ мажоритарного элемента, приведена на рисунке 3. Схема состоит из 8 элементов, имеющих общее количество входов 19. Количество входов характеризует сложность схемы и называется «Число по Квайну». Схема составленная на основе функции СКНФ, также будет иметь 19 входов. 2.3 Понятие базиса Любая, сколь угодно сложная логическая функция, представленная таблицей истинности, может быть представлена в форме СДНФ или СКНФ. Каждая из этих формул записана с помощью логического сложения, умножения и отрицания. Поэтому для реализации логических устройств, предназначенных для обработки цифровых сигналов, в общем случае необходимо иметь элементы, выполняющие операции И, ИЛИ, НЕ. Такой набор элементов называется функционально полной системой логических элементов или логическим базисом. Это означает, что из комбинации логических элементов И, ИЛИ, НЕ, взятых в достаточном количестве, можно построить сколь угодно сложное цифровое устройство. Базис из элементов: И, ИЛИ, НЕ называется основным. Однако, число необходимых элементов в такой системе можно уменьшить, исключив из неё либо элемент ИЛИ, либо элемент И. Например, в соответствии с теоремой де Моргана, имеем 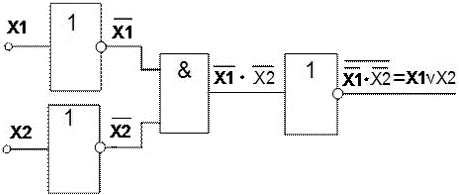 Рисунок 4 Реализация элемента ИЛИ на элементах НЕ, И Аналогично можно исключить элемент И, заменив его операцией логической суммы над инверсными значениями переменных с последующим применением операции инверсии При схемной реализации функционально полных систем с минимальным логическим базисом идут по пути использования универсальных логических элементов: ИЛИ-НЕ, И-НЕ и И-ИЛИ-НЕ (Рисунок 5). 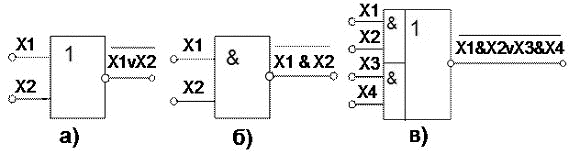 Рисунок 5 Универсальные логические элементы Элемент ИЛИ-НЕ Рисунок 5,а) осуществляет логическую операцию Элементы универсальных базисов позволяют реализовать все три основные логические операции (Рисунок 6). Например, для осуществления операции НЕ с помощью элемента И-НЕ достаточно объединить входы 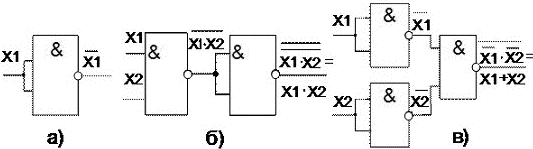 Рисунок 6 Реализация функций НЕ, И и ИЛИ на элементах И-НЕ При последовательном соединении элемента И-НЕ и инвертора осуществляется операция логического умножения: Применение трёх элементов И-НЕ, два из которых работают в режиме инвертирования с объединёнными входами (рисунок 6,в), позволяют реализовать операцию логического сложения В общем случае логическая функция Y может зависеть от нескольких переменных X1,X2,…,Xn. Говорят, что функция Y определена, если известны её значения для всех возможных наборов переменных. Функция Y не определена, когда некоторые сочетания переменных по условию задачи невозможны. В этом случае её можно доопределить, приписав ей значение «1» либо «0» по соображениям удобства реализации. 2.4 Минимизация логических формул Однозначная зависимость сложности логической формулы и функциональной схемы логического устройства приводят к выводу необходимости минимизации структурной формулы логического устройства. Минимизация осуществляется с использованием основных соотношений, законов и теорем алгебры логики. 2.4.1 Расчётный метод минимизации Применение этого метода состоит в последовательном применении к некоторой формуле законов и правил тождественных преобразований алгебры логики. При этом широко используют следующие приёмы: прибавление одного или нескольких членов, входящих в СДНФ, поскольку X ∨ X ∨ X = X; выделение членов, содержащих множитель Пример: Минимизировать функцию СДНФ мажоритарного элемента (См. п.2.2) и реализовать его схему на элементах основного базиса. 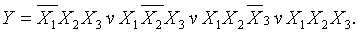 Склеивая первые три минтерма с четвёртым, получаем ДНФ функции мажоритарного элемента, которая проще СДНФ: Y = X1·X2 ∨ X1·X3 ∨ X2·X3 Минимизированная функциональная схема мажоритарного элемента приведена на рисунке 7. 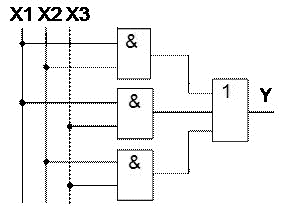 Рисунок 7 Функциональная схема мажоритарного элемента, реализованная на основе минимизированной функции ДНФ Из сравнения схем, приведённых на рисунках 3 и 7 следует, что в минимизированной схеме число по Квайну уменьшилось с 19 до 9. Метод минимизирующих карт КарноКарты Карно — это графическое представление таблиц истинности логических функций. Они содержат по 2n ячеек, где n — число логических переменных. Например, карта Карно для функции трёх переменных содержит 2n=23=8 ячеек, для четырёх переменных — 24=16 ячеек. Карта размечается системой координат, соответствующих значениям входных переменных. Обратим особое внимание на то, что координаты столбцов (а также и строк, если n>3), следуют не в естественном порядке возрастания двоичных кодов, а так: 00 01 11 10. Это делается для того, чтобы соседние наборы (в том числе и столбцов 1 и 4) отличались лишь одной цифрой в каком-либо разряде. Процесс минимизации заключается в формировании правильных прямоугольников, содержащих по 2k ячеек, где k — целое число. В прямоугольники объединяются соседние ячейки, которые соответствуют соседним элементарным произведениям (т. е. отличаются только в одном разряде). Несмотря на то, что карты Карно изображаются на плоскости, соседство квадратов устанавливается на поверхности тора. Верхняя и нижняя границы карты как бы склеиваются, образуя поверхность цилиндра. При склеивании боковых границ получается поверхность тора. Пример: Минимизировать функцию трёх переменных, заданную таблицей истинности (таблица 6). Таблица 6 Таблица истинности функции трёх переменных
СДНФ функции: Составляем карту Карно и производим разметку её сторон: 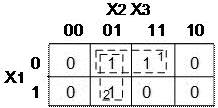 Рисунок 8 Карта Карно функции 3-х переменных. На карте Карно формируем два прямоугольника. Первый из них объединяет (как бы заключает в скобки) два первых минтерма (слагаемых), а второй — первое и третье слагаемые СДНФ минимизируемой функции, приведённой выше. Минтермы, объединённые в прямоугольники, отличаются только в одном разряде. Их неизменяемая часть, которая при минимизации расчётным методом выносится за скобки, и является минимизированным значением функции: 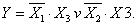 Таким образом, карта Карно позволяет поместить рядом, то есть в соседних ячейках, соседние элементарные произведения, отличающиеся только одним сомножителем. Последовательность действий при минимизации: 1 Изображается карта Карно и производится разметка её сторон. 2 Ячейки карты Карно, соответствующие наборам переменных, обращающих функцию в «1», заполняются единицами, остальные — нулями. 3 Выбирается наилучшее покрытие карты прямоугольниками. Наилучшим считается покрытие, образованное минимальным числом прямоугольников, а если таких вариантов несколько, то выбирается тот, который даёт максимальную площадь прямоугольников. Пример: Минимизировать функцию четырёх переменных, представленную картой Карно: (Рисунок 9). 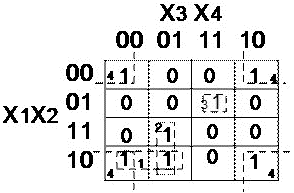 Рисунок 9 Карта Карно функции 4-х переменных Из карты Карно записываем минимизированное значение функции: 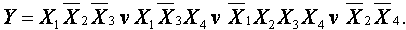 2.4.2 Минимизация неопределённых логических функций Если функция имеет запрещённые наборы входных переменных, при которых функция может иметь произвольное значение (0 либо 1), то такая функция называется неопределённой. Для удобства минимизации её следует доопределить, то есть неопределённые значения карты Карно произвольным образом заменить «1» либо «0». Если функция имеет m запрещённых наборов, то может быть 2m вариантов доопределения. Следует выбрать тот вариант, при котором минимизированная функция будет более простой. 2.5 Запись структурных формул в универсальных базисах Запись в базисе И-НЕ производится в два этапа: а) Логическая формула, минимизированная в основном базисе, представляется в форме ДНФ. б) Над правой частью полученной формулы ставится два знака инверсии и с помощью формул де Моргана осуществляется переход в базис И-НЕ. Пример. Записать в базисе И-НЕ минимизированную функцию мажоритарного логического элемента:также производится в два этапа: 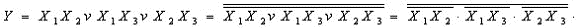 Запись в базисе ИЛИ-НЕ а) Логическая функция, минимизированная в основном базисе, представляется в форме КНФ. б) Над правой частью полученной формулы ставятся два знака инверсии, и с помощью формул де Моргана производится переход в базис ИЛИ-НЕ. Пример: 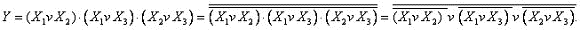 Запись в базисе И-ИЛИ-НЕ производится также в два этапа: а) Логическая формула для инверсного значения функции б) Для перехода к базису И-ИЛИ-НЕ над обеими частями формулы ставится один знак инверсии, и с помощью формул де Моргана производится переход в базис И-ИЛИ-НЕ. |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Главная | Контакты | Нашёл ошибку | Прислать материал | Добавить в избранное |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

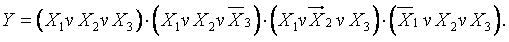
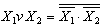 . Отсюда следует, что операцию логического ИЛИ можно заменить операцией И над инверсными значениями переменных,
. Отсюда следует, что операцию логического ИЛИ можно заменить операцией И над инверсными значениями переменных, 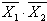 , а затем к результату применить операцию инверсии
, а затем к результату применить операцию инверсии 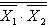 и тем самым исключить элемент ИЛИ (Рисунок 4).
и тем самым исключить элемент ИЛИ (Рисунок 4).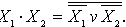 Следовательно, системы, состоящие из двух элементов(ИЛИ, НЕ либо И, НЕ), также являются функционально полными системами и содержат минимальный логический базис.
Следовательно, системы, состоящие из двух элементов(ИЛИ, НЕ либо И, НЕ), также являются функционально полными системами и содержат минимальный логический базис.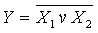 , называемую также стрелкой Пирса. Элемент И-НЕ (Рисунок 5,б) осуществляет логическую операцию
, называемую также стрелкой Пирса. Элемент И-НЕ (Рисунок 5,б) осуществляет логическую операцию 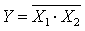 и называется штрих Шеффера. Элемент И-ИЛИ-НЕ (Рисунок 5,в) осуществляет операцию
и называется штрих Шеффера. Элемент И-ИЛИ-НЕ (Рисунок 5,в) осуществляет операцию 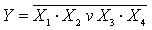 и является элементом сложного базиса.
и является элементом сложного базиса.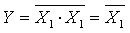 (рисунок 6,а). Аналогично и для элемента ИЛИ-НЕ.
(рисунок 6,а). Аналогично и для элемента ИЛИ-НЕ.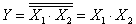 (рисунок 6,б). Такое же соединение элементов ИЛИ-НЕ реализует операцию логического сложения:
(рисунок 6,б). Такое же соединение элементов ИЛИ-НЕ реализует операцию логического сложения: 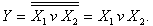
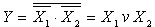 . Соединение трёх логических элементов ИЛИ-НЕ позволяет реализовать операцию логического умножения
. Соединение трёх логических элементов ИЛИ-НЕ позволяет реализовать операцию логического умножения 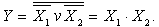
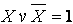 ; использование правила склеивания и др. Получающаяся в результате минимизации алгебраическая формула называется тупиковой. Функция может иметь несколько тупиковых форм.
; использование правила склеивания и др. Получающаяся в результате минимизации алгебраическая формула называется тупиковой. Функция может иметь несколько тупиковых форм. 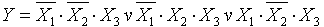
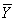 минимизируется в основном базисе и представляется в форме ДНФ.
минимизируется в основном базисе и представляется в форме ДНФ.