• Главная
• Контакты
• Нашёл ошибку
• Прислать материал
• Добавить в избранное

Роль статистических методов при сертификации определяется их местом при разработке системы качества. Стандарт ИСО 9004.2 – 91 (п. 6.4.3) устанавливает, что статистические методы могут быть полезны в большинстве случаев при сборе данных и их применении, идет ли речь о достижении лучшего понимания запросов потребителей (в процессе контроля, изучения возможностей, прогнозирования) или об измерении качества для облегчения принятия решений.

Пункт 20.1 стандарта ИСО 9004 характеризует статистические методы как один из важнейших элементов систем качества на всех стадиях «петли качества». В частности, стандарт ИСО 9004 рекомендует применять статистические методы при:

•анализе рынка продукции (услуги);

• проектировании (разработке) продукции (услуги);

• определении требований к продукции (услуге);

• изучении возможностей продукции (услуги);

• анализе данных (дефектов).

Таким образом, документация, относящаяся к статистическим методам, является эффективным средством демонстрации соответствия системы качества требованиям стандартов ИСО серии 9000. Иными словами, статистические методы могут рассматриваться как индикатор (признак) системы качества.

При проверке системы качества эксперт-аудитор или лицо, проводящее проверку, имеет возможность: применить статистические методы при проверке системы качества для оптимизации плана и процедур проверки; проанализировать документацию, относящуюся к статистическим методам, для проверки наличия элементов системы качества.

Стандарты ИСО серии 9000 рекомендуют использовать следующие статистические методы:

• планирование экспериментов (факторный анализ);

• анализ дисперсий (дисперсионный анализ);

• оценка безопасности (анализ рисков);

• критерии значимости;

• контрольные карты;

• выборочный статистический контроль.

Для выбора метода, наиболее адекватного условиям сертификации, целесообразно рассмотреть возможные схемы сертификации, а затем проанализировать возможные статистические методы, пригодные для задач сертификации.

Руководство ИСО/МЭК 28 «Общие правила для модели системы сертификации продукции третьей стороной» предусматривает 8 основных схем сертификации.

Анализ позволяет определить те статистические методы, которые целесообразно использовать в той или иной схеме сертификации.

Характерная особенность схем № 1–4 состоит в том, что они базируются на типовом испытании и последующей периодической проверке сертифицированной продукции (схемы № 2–4).

Как правило, типовое испытание осуществляется на единственном образце и, следовательно, статистические методы в этой ситуации неприменимы для большинства показателей качества сертифицируемой продукции. Однако для некоторых изделий в число показателей, которые подлежат проверке при сертификационных испытаниях (по схемам № 1–4), могут входить статистические (например, для приборов времени таким показателем является среднесуточная погрешность хода). Проверка таких показателей осуществляется наиболее эффективно с использованием методов математической статистики.

Кроме того, в схемах сертификации № 2–4 предусмотрен периодический контроль за сертифицированной продукцией. Этот периодический контроль может быть организован двумя способами.

Способ 1. Сопоставление показателей качества, оцененных при периодических испытаниях на одном образце, с теми, которые зафиксированы при типовом испытании. Решающее правило в этом случае выглядит следующим образом:

• результаты проверки признаются положительными, если для всех показателей R_i (i = 1…, n) R_iТ ? R_iП;

• результаты проверки признаются отрицательными, если существует хотя бы один показатель для которого R_iТ ? R_jП.

Здесь R_iТ ? R_jП – символ отношения: «R_iТ» не хуже «R_jП»; R_iТ – значение показателя, определенное при типовом испытании; R_jП – значение показателя, определенное при периодическом контроле.

Для статистических показателей, получаемых при периодических испытаниях на одном образце, статистический подход оправдан.

Способ 2. Сопоставление показателей качества, определенных при периодических испытаниях образцов, отобранных из находящихся на складе потребителя и (или) поставщика, с нормативными значениями, регламентированными в стандарте. В этом случае, независимо от природы показателей качества, применять статистические методы целесообразно.

Схема сертификации № 5 характерна тем, что в ней присутствуют элементы схем № 1–4 и, следовательно, варианты применения статистических методов для этой схемы подобны рассмотренным выше. Кроме того, для этой схемы принята сертификация (проверка) системы качества производства сертифицируемой продукции. Сертификация системы качества обычно осуществляется путем проведения экспертиз и конкретных проверок, включающих анализ показателей точности и стабильности технологического процесса [4].

Формирование плана проверок безопасности также может быть осуществлено с применением статистических методов. Однако к настоящему времени разработано несколько эффективных количественных методов анализа безопасности, которые опираются на статистическую методологию и пригодны для целей сертификации [5–7].

В соответствии с положениями стандартов ИСО серии 9000 статистические методы применяются на всех стадиях «петли качества» и, таким образом, проверка систем качества (схемы № 5 и 6) должны включать статистические методы и документацию, относящуюся к ним.

Схема сертификации № 7 целиком опирается на выборочную проверку партии сертифицируемой продукции и, значит, для этой схемы статистические процедуры являются наиболее адекватными при принятии решения.

При сертификации каждого образца по схеме № 8 применение статистических методов возможно при проверке статистических показателей.

Итог проведенного анализа применения статистических методов в зависимости от схемы сертификации дан в табл. 5.1.

Таблица 5.1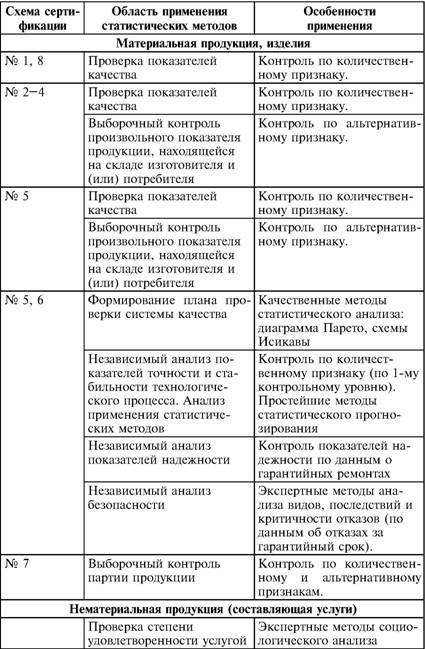

При сертификации услуги целесообразно исходить из условной формулы:

Сертификация (услуги) = сертификация (материальной продукции) + + сертификация (нематериальной составляющей). (5.1)

Формально сертификация материальной продукции, порождаемой услугой (первая составляющая в 5.1) опирается на схемы № 1–8, для которых применение статистических методов рассмотрено выше.

Сертификация нематериальных аспектов услуги предполагает проверку таких характеристик, как чуткость, вежливость, скорость обслуживания и т. п., требования к которым должны быть сформулированы в соответствующем нормативном документе. Анализ (проверка) этих характеристик возможен только с использованием экспертных методов, являющихся частными случаями статистических.

В связи с тем, что в основе статистических методов лежат положения теории вероятностей и математической статистики, которые недостаточно глубоко освоены инженерно-техническим персоналом предприятий, ниже рассматриваются только простейшие статистические методы, применяемые при сертификации систем качества. К числу простейших будем относить те, которые отвечают следующим условиям: минимально используют математический аппарат; допускают простую инженерную интерпретацию; графическое отображение.

В силу своей простоты эти методы могут легко использоваться при сертификации систем качества, что делает их привлекательными для практики.

Диаграмма «причины – результат» предложена проф. Каору Исикава (Япония) для структуризации отношений между некоторым заранее определенным показателем качества и множеством факторов, которые могут влиять на этот показатель. Эта диаграмма (рис. 5.1) строится в следующей последовательности [2]:

1) определяется цель анализа и выделяется показатель качества, подлежащий исследованию;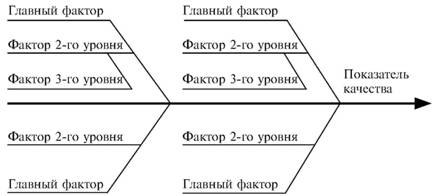

Рис. 5.1

2) выделяются главные причины, влияющие на данный показатель качества в первую очередь (главные факторы);

3) выделяются вторичные причины (факторы), влияющие на главные, которые называют факторами 2-го уровня;

4) выделяют факторы 3-го уровня, влияющие на факторы 2-го уровня.

К числу достоинств данной диаграммы следует отнести:

• возможность вовлечения большого числа факторов для анализа (до 4–6 главных факторов, до 6 факторов 2-го уровня на каждый главный, до 8 факторов 3-го уровня на каждый фактор 2-го уровня);

• наглядность представления анализа;

•достаточно независимая классификация факторов, позволяющая избежать их пересечения, что удобно для анализа.

Диаграмма «причина – результат» дает возможность определить основные направления создания системы качества и соответственно основные направления анализа системы качества при ее сертификации. Еще раз следует отметить, что документация, содержащая диаграммы «причины – результат» для различных ситуаций, являются индикатором наличия элементов системы качества на предприятии, а также источником информации для формирования плана проверки предприятия.

Диаграмма «причины – результат» может быть построена экспертами-аудиторами, осуществляющими проверку предприятия, для определения «узких» мест системы качества при будущей проверке.

В качестве примера рассмотрим последовательность построения диаграммы «причины – результат» при анализе системы качества ремонтного предприятия. Исследуемым показателем качества ремонта выбрана задержка в ремонте. На следующем этапе определяют главные факторы, связанные с выбранным показателем. К их числу относят:

1. Объект ремонта.

2. Склад.

3. Оборудование.

4. Рабочие.

5. Технология ремонта.

К числу факторов 2-го уровня можно отнести:

1.1. Техническое состояние объекта ремонта.

1.2. Дефекты.

2.1. Запасные части.

2.2. Документооборот.

3.1. Техническое состояние оборудования.

3.2. Оснастка.

4.1. Квалификация.

4.2. Здоровье.

5.1. Диагностирование.

5.2. Документация.

Для каждого фактора 2-го уровня выделяют фактор 3-го уровня, например:

1.1.1. Срок эксплуатации объекта ремонта.

2.1.1. Поставка запасных частей.

3.1.1. Срок эксплуатации оборудования.

4.1.1. Обучение.

5.1.1. Программа дефектации.

Полученные результаты оформляются в виде диаграммы, рис. 5.2. Для задачи сертификации эту диаграмму можно использовать следующим образом:

• сформулировать 5 направлений проверок: объект ремонта, склад, технология ремонта, персонал, оборудование;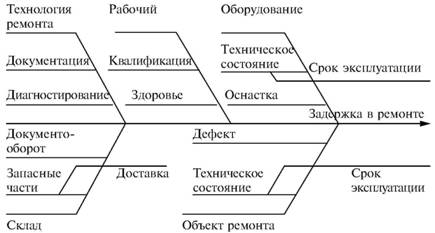

Рис. 5.2

• по каждому направлению организовать проверки согласно классификации по факторам 3-го уровня.

Важно отметить, что в силу особенностей классификации (структурирования) проверяющие не будут мешать друг другу, так как их проверки опираются на разную исходную информацию, нормативную документацию и т. д.

На практике (для построения схемы Исикавы) часто применяют правило «пяти М» для выделения главных факторов [8]. Оно состоит в том, что, как правило, существенными факторами, влияющими на качество, являются: материалы; машины (оборудование); технология (методы); измерения; персонал.

Все эти слова по-английски начинаются с буквы «М», откуда и произошло название этого правила. Дж. Харрингтон [9] добавляет еще два главных фактора: финансы и руководство.

При необходимости каждый из факторов на схеме Исикавы может быть подвергнут, в свою очередь, причинно-следственному анализу, что значительно расширяет возможности этой диаграммы.

Цель построения диаграммы Парето – выделение главных (доминирующих) однородных факторов, влияющих на качество продукции или услуги.

Область применения диаграммы Парето для целей сертификации примерно такая же, как и предыдущей. Разница в том, что анализу подвергаются однородные факторы. Эффективность диаграммы состоит в том, что с ее помощью из большого числа факторов просто и в наглядной форме выделяется часть факторов, влияющих непосредственно на качество.

Диаграмма Парето представляет собой столбчатую диаграмму, по горизонтальной оси которой откладывают наименования анализируемых факторов (признаков) в определенном порядке, а по вертикальной – значения каждого из факторов в безразмерных единицах (%) или размерных единицах, общих для анализируемых признаков.

Порядок построения диаграммы Парето:

1) выделяют факторы (признаки), подлежащие анализу;

2) определяют период сбора данных;

3) проводят сбор данных. Для реализации этого этапа надо иметь четкую цель (мотивацию) и соответствующие ресурсы;

4) заполняют соответствующие учетные формы;

5) обрабатывают данные;

6) делают выводы.

Например, необходимо выделить наиболее «дефектоносные» агрегаты автомобиля некоторой марки, для того чтобы проверить правильность подбора испытательных стендов, размещения рабочих участков и выделить «узкие» места ремонта автомобиля.

Для решения этой задачи:

1) выделяем признаки – агрегаты автомобиля: двигатель; трансмиссия; ходовая часть; рулевое управление; тормозная система; кузов; электрооборудование.

2) определяем период сбора данных – 6 месяцев.

3) по данным возврата автомобилей после ремонта (дефектным ведомостям) определяем число дефектов, приходящееся на каждый агрегат (n!). Общее число дефектов N = 100.

Результаты наблюдений фиксируем в специальном учетном листке (табл. 5.2). Если бы диаграмму Парето строил персонал ремонтного предприятия, то табл. 5.2 при аудите могла бы рассматриваться как исходная документация типа протокола испытаний, относящаяся к документации системы качества;

4) заполняем соответствующую таблицу для построения диаграммы Парето (табл. 5.3), используя данные табл. 5.2. При этом первая строка содержит информацию об агрегате с максимальным числом дефектов; далее – по нисходящий.

Если накопленная сумма дефектов будет отличаться от величины N или накопленная сумма процентов будет отличаться от 100 %, то в вычисление вкралась ошибка. Последнее возможно

Таблица 5.2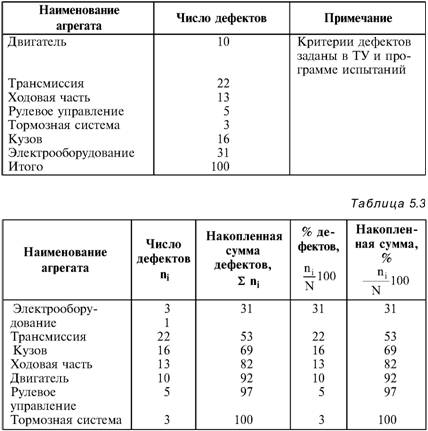

в связи с округлением. По данным, приведенным в табл. 5.3, строится диаграмма Парето, содержащая:

• горизонтальную ось, на которой в том же порядке, что и в табл. 5.3, нанесены наименования агрегатов;

• левую вертикальную ось, на которой в соответствующем масштабе отложено суммарное число дефектов (максимальное значение отрезка левой вертикальной оси равно N);

• правую вертикальную ось, на которой в соответствующем масштабе отложены значения накопленного процента дефектов (максимальное значение отрезка правой вертикальной оси равно 100 %).

Максимальные значения левой и правой вертикальных осей, очевидно, равны между собой. В построенных осях диаграммы откладывают число дефектов агрегатов в соответствующем масштабе в виде «столбиков» и накопленный процент дефектов.

Пример диаграммы Парето для данных табл. 5.3 приведен на рис. 5.3. Из анализа диаграммы следует, что около 70 % дефектов приходится на 3 системы автомобиля: электрооборудование, трансмиссия, кузов. Таким образом, для эксперта-аудитора эта диаграмма Парето дает информацию о правильности подбора стендов, размещении участков диагностирования и тех «узких» местах производства, которые должны быть охвачены системой качества.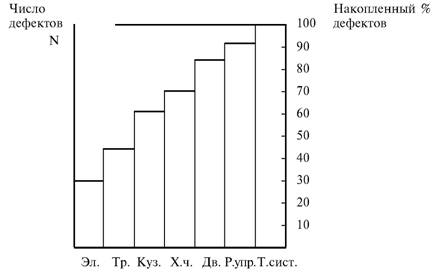

Рис. 5.3

Следует отметить, что диаграмма Парето для отдела качества ремонтного предприятия является информацией о первоочередных мероприятиях по управлению (повышению) качества ремонта автомобиля. Для данного примера система мероприятий должна строиться таким образом, чтобы в нее были включены 3 выделенных агрегата автомобиля.

Диаграммы Парето целесообразно строить по нескольким признакам, тогда они несут много разнородной информации, что важно для всесторонней оценки системы качества при аудите:

1) потери (затраты) времени, труда, средств;

2) себестоимость продукции (ремонта);

3) персонал;

4) безопасность;

5) технологические операции;

6) несоответствия;

7) участки предприятия;

8) сырье и т. п.

Рассмотрим еще один пример, демонстрирующий эффективность анализа качества с использованием диаграммы Парето.

Исследуется качество работы двух ремонтных участков, каждый из которых обслуживает по два ремонтных и диагностических стенда. Качество работы участков оценивают по числу дефектов трех типов (Д1, Д2, Д3), выявленных за 4 месяца работы.

Результаты наблюдений представлены в табл. 5.4.

Таблица 5.4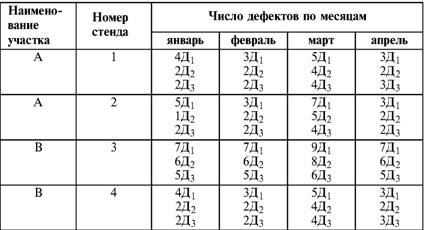

Примечание. Запись АД_i– (i = 1, 2, 3) означает, что зафиксировано А дефектов типа Д;.

Из анализа табл. 5.4 следует, что:

• если построить диаграмму Парето по участкам, то можно сделать вывод о том, что качество работы участка В хуже, чем участка А;

• если построить диаграмму Парето по стендам, то можно сделать вывод о том, что качество работы стенда 3 хуже, чем остальных стендов. Следовательно, проблема качества связана не с участком В, а со стендом 3;

• если построить диаграмму Парето по видам дефектов, то можно сделать вывод, что дефект Д1 встречается наиболее часто. Таким образом, второй аспект повышения качества обусловлен снижением числа дефектов Д1. Этот вывод устойчив и не зависит от вида стенда;

• если построить диаграмму по месяцам работы, то можно сделать вывод, что наиболее неблагополучным в аспекте качества является третий месяц. Эта информация подлежит дальнейшему анализу для устранения причин дефектов.

В некоторых случаях целесообразно строить совместно диаграмму Парето и схему «причины – результаты» для выделения «узких» мест системы качества, формирования плана проверок и ранжирования факторов, влияющих на качество.

В заключение этого раздела следует остановиться на идее визуализации (наглядности) анализа качества. Сравнивая табл. 5.3 и рис. 5.3, можно сказать, что каждая из этих форм содержит одну и ту же информацию о качестве. Однако, глядя на табл. 5.3 (которая содержит данные только по семи агрегатам), можно сказать, что «глаза разбегаются» от обилия цифр. В отличие от этого, диаграмма Парето (рис. 5.3) сразу показывает наиболее «дефектонос-ные» агрегаты, что, в свою очередь, дает импульс специалистам для дальнейшего анализа.

Цель применения простейшего корреляционного анализа – определить и оценить линейную связь между фактором и показателем качества. При этом предполагается, что:

• связь между показателем качества и фактором случайная;

• значения показателя качества и фактора, который, возможно, влияет на него, имеют нормальное распределение вероятностей.

Типичные варианты исследования связи:

• показатель качества ремонта – себестоимость ремонта;

• затраты на ремонт – доремонтный ресурс;

• затраты на ремонт – квалификация рабочих;

• ресурс между ремонтами – год выпуска изделия;

• затраты на диагностическое оборудование – показатель качества ремонта.

Обнаружение связи или доказательство ее отсутствия между фактором X и показателем качества Y дает возможность объективно оценить проверку элементов системы качества. Например, если связь между показателем качества ремонта и квалификацией рабочих не обнаруживается, то это говорит о том, что проверка персонала этого объекта может быть ослаблена.

Для предприятия, внедряющего систему качества, использование методов корреляционного анализа дает возможность осознанно (на основе данных, а не инженерной интуиции) реали-зовывать мероприятия по управлению качеством продукции.

Например, исследование связи между метрологической характеристикой стенда для диагностирования тормозных качеств X и процентом возврата автомобилей после ремонта (по причине низкого качества тормозной системы) Y показало, что нецелесообразно управлять качеством ремонта тормозной системы за счет улучшения характеристик диагностического стенда.

Визуализацию корреляционного анализа осуществляют с использованием диаграмм рассеяния.

Порядок построения диаграммы рассеяния:

1) определяют показатель качества Y, подлежащий анализу, и параметр X, влияющий на этот показатель;

2) уточняют инженерные аспекты этой связи, т. е. физическую возможность зависимости Y (показателя качества) от параметра X;

3) определяют период наблюдений, на котором собирают данные о значениях X и соответствующих значениях Y. Таким образом, формируются два массива данных: Х₁, Х₂…., Х_п; Y₁, Y₂,…, Y_n. Для повышения достоверности данных целесообразно, чтобы n ? 20;

4) строят координатную сетку: по горизонтали – ось, на которой откладывают в соответствующем масштабе значения X; по вертикали – значения Y.

Масштабы следует подобрать таким образом, чтобы значения Х_i; (i = 1, 2…., n) и значения Y_i (i = 1, 2…., n) лежали в одинаковых диапазонах, т. е. точки с координатами (Х/, Y,) были заключены в некотором квадрате;

5) на координатную сетку наносят точки с координатами (Х_i, Y_i;) (i = 1, 2…., n), при этом возможны следующие основные варианты расположения точек (рис. 5.4):

• на рис. 5.4 а положительная корреляция (связи) между параметром X и показателем качества Y;

• на рис. 5.4 б отрицательная корреляция (связи) между параметром X и показателем качества Y;

• на рис. 5.4 в отсутствует линейная связь между параметром X и показателем Y;

• на рис. 5.4 г отсутствует линейная связь между X и Y, но есть некоторая криволинейная связь между этими характеристиками.

Следует отметить, что чем теснее линейная связь между характеристиками X и Y, тем ближе точки (Х_i, Y_i) концентрируются около некоторой прямой. Если между фактором X и показателем качества Y связь функциональная (т. е. не случайная), то точки (Х_i, Y_i) лежат строго на прямой.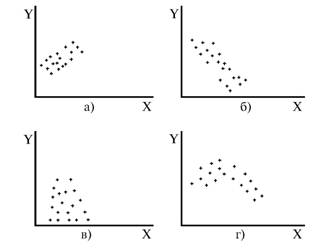

Рис. 5.4

Для объективизации этого анализа рекомендуется вычислять коэффициент корреляции r, характеризующий тесноту линейной связи: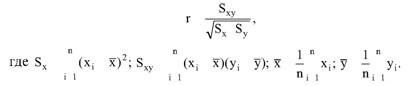

Если |г| > 1, это значит, что допущена ошибка в вычислениях, если

, то между Х и Y не выявлена линейная связь.

Если r близок K + 1, это значит, что между фактором Х и показателем Y существует положительная линейная связь, т. е. с увеличением параметра Х увеличивается показатель качества Y; если r близок K – 1, это значит, что между фактором Х и показателем Y существует отрицательная линейная связь, т. е. с увеличением параметра Х уменьшается показатель качества Y.

Для того чтобы убедиться в отсутствии линейной связи между рассматриваемыми факторами, что в рамках математической статистики означает проверку статистической гипотезы r = 0, используют специальный критерий, т. е. проверку условия [10]: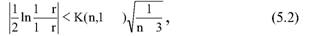

где K (n, 1 – ?) – коэффициент, зависящий от объема n выборки и доверительной вероятности (0,5 <1 – ?< 1).

Коэффициент K (n, 1 – ?) называют квантилем распределения Стьюдента для доверительной вероятности (1 – ?) и числа (n – 1) степеней свободы. Этот коэффициент определяют по таблицам [11] с двумя входами n и 1 —?.

Например, для

n = 10; ? = 0,1; K (n, 1 —?) = 1,812;

n = 20; ? = 0,1; K (n, 1 —?) = 1,725.

Если справедливо неравенство (5.2), то с достаточно большой вероятностью 1 – ? > 0,5 можно считать, что коэффициент корреляции равен нулю, т. е. факторы линейно независимы.

Если отвергается гипотеза r = 0, то это значит, что между факторами имеется линейная связь. Для лица, проводящего аудит, это означает возможность проверки только одного фактора, информация о котором может быть получена наиболее просто в ходе проверки.

Сертификация систем качества на соответствие стандартам ИСО серии 9000 предполагает оценку (анализ) точности и стабильности производственных процессов (ПП). Такая оценка может быть выполнена с использованием индексов воспроизводимости ПП, которые получили широкое распространение в практике сертификации технологического оборудования автомобильных корпораций США и Японии.

Индексом воспроизводимости ПП (в предположении, что значение параметра ПП (детали) распределено нормально) называют характеристику С_р: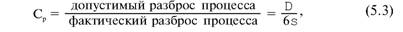

где ? – среднее квадратическое отклонение значений параметра детали от среднего значения; D – допустимый разброс (допуск).

В формуле (5.3) предполагается, что среднее значение процесса находится в середине поля допуска. Фактически С_р соотносит допуск на параметр детали с фактическим разбросом. Таким образом, если С_р = 1,0, то ПП можно признать воспроизводимым в том смысле, что ПП обеспечивает установленные требования к качеству детали. Так как на практике значение у оценивается по выборке измерений параметра детали с определенными погрешностями, значение С_р = 1,0 обычно не используется в качестве критического (минимально приемлемого).

Как показывают расчеты вероятности выхода значений параметра детали за границы поля допуска, т. е. вероятности брака, если:

• С_р > 1,67, то имеется существенный запас качества по сравнению с требованиями допуска (возможно сужение поля допуска);

•1,33 < С_р ?1,67 – нормальное состояние процесса (вероятность брака 0,007 %);

1 < С_р ? 1,33 – вероятность брака близка к 0,3 %;

0,67 < С_р ? 1 – вероятность брака близка к 4,5 % (необходимы меры по повышению стабильности и качества процесса);

• С_р ? 0,67 – процесс неконтролируем.

Для практических целей следует указать необходимый объем выборки для принятия решений относительно С_р. В статистическом смысле эта задача может быть сформулирована следующим образом: проверить гипотезу Н₀: C_p ? Cp* (процесс невоспроизводим) против альтернативы Н₁: С_р > C_p* (процесс воспроизводим).

Если обозначить ? – риск поставщика, ? – риск потребителя, то объем выборки N, обеспечивающий непревышение значений ? и ? при принятии решений относительно C_p, может быть найден по формуле: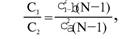

где c²q(N-1) – квантиль, x²– квадрат распределения с числом (N—1) степеней свободы для вероятности ?; С₁,С₀ – безусловно приемлемый и безусловно неприемлемый уровень C_p для данного ПП.

Другими словами, ? – это вероятность признания процесса невоспроизводимым (C_p ? C_p*) при условии, что реальный индекс воспроизводимости не меньше С₁; ? – это вероятность признания процесса воспроизводимым (С_р > C_p *) при условии, что фактический индекс воспроизводимости не больше С₀.

Критическое значение C_p* для принятия решения определяется: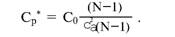

В табл. 5.5 приведены значения С₁ / С₀ и С_р * / С₀ для разных значений N и ? = ?=0,1 и ? = ?=0,05.

Рассмотрим пример использования табл. 5.5. Определим объем N выборки и критическое значение С_р * для принятия решения относительно C_p для ? = ? = 0,1; С₁ = 1,43; С₀ = 1,1, т. е. С₁ / С₀ = 1,3.

По табл. 5.5 находим N = 50 (колонка 1) и С_р * / С₀ = 1,13 (колонка 3). Откуда С_р * = 1,24.

Таким образом, при объеме выборки N = 50 и критическом значении С_р * = 1,24 в 10 % случаев процесс может быть признан невоспроизводимым при С_р > 1,43 и в 10 % случаев процесс может быть признан воспроизводимым при С_р ? 1,1.

Таблица 5.5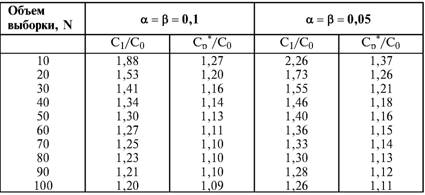

В случае односторонних допусков рассматривают индексы: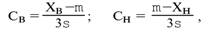

где м – среднее значение параметра; Хв (Хн) – верхняя (нижняя) граница допуска.

Очевидно, что при С_в = 1,0 (С_н = 1,0) вероятность производства бракованных деталей по данному параметру равна половине (0,135 %) по сравнению с тем, что обеспечивает С_р = 1,0 в случае с двусторонним допуском (0,27 %).

Область применения введенных индексов воспроизводимости – оценка стабильности технологического процесса производства изделия с целью сертификации процесса или системы качества.

В качестве нормы индекса целесообразно устанавливать С_р = = 1,33, который обеспечивает низкий уровень брака.

Данный метод анализа систем качества может быть использован при аудите отдельных операций технологического процесса. Основная цель применения индексов воспроизводимости – удобная свертка информации в ПП в наиболее подходящей форме. Эти показатели определяют, имеет ли ПП достаточно низкую изменчивость и удовлетворяет ли допускам процесса или существует проблема настройки.

Как отмечается в [4], наибольшая ценность этих показателей – в поддержке усилий, направленных на предотвращение брака, а также в реализации мониторинга ПП, что обеспечивает получение «истории» качества для аудита.

Сертификация в соответствии со схемой № 7 (табл. 5.1) предполагает проведение выборочного контроля (испытания выборки, отобранной из партии сертифицируемой продукции).

Сертифицируемой партией продукции называют одновременно представленную для сертификации (испытаний) совокупность единиц продукции одного наименования, типономинала или типоразмера и исполнения, произведенной в течение одного интервала времени.

Объем партии – число единиц продукции, составляющих сертифицируемую партию.

Выборка – это единицы продукции, отобранные из сертифицируемой партии для испытаний; объем выборки – число единиц продукции, составляющих выборку.

Формирование сертифицируемой партии – это процесс отбора (комплектации) необходимого и достаточного (возможного) числа единиц продукции для проведения сертификации. Формирование выборки от сертифицируемой партии продукции представляет процесс отбора необходимого и достаточного числа единиц продукции для проверки качества из сертифицируемой партии.

Задача формирования сертифицируемой партии продукции и выборки из нее актуальна только при использовании схемы сертификации № 7.

Формирование партии продукции имеет большое значение для практики сертификации, так как во многом предопределяет процедуру контроля, представительность (репрезентативность) выборки и результаты сертификации.

Классификация факторов, влияющих на объем сертифициру-емой партии продукции, представлена на рис. 5.5.

При формировании партии для сертификации необходимо со-блюдать один из следующих принципов: независимость единиц продукции (элементов) в партии; независимость функциониро-вания элементов в структуре изделий, формирующих партии; максимальную однородность свойств изделий в партии.

При комплектации партии по принципу независимости (ста-тистической однородности) единиц продукции в партии объем может быть установлен заранее, до начала производства.

Комплектация партии по принципу независимости функциони-рования элементов в структуре изделий (функциональная однород-ностъ) производится после сборки изделий, каждое из которых со-стоит из последовательно соединенных независимых элементов, по-ставляемых партиями объемом N единиц, сформированных, в свою очередь, по принципу независимости элементов в партии.

Комплектация партий по третьему принципу связана с соблю-дением следующих требований: каждое изделие комплектуемой партии должно быть изготовлено из одной и той же партии сырья («сырьевая» однородность), по одной и той же технологии, на од-ном и том же оборудовании («технологическая» однородность). В случае невозможности соблюдения принципа однородности партии продукции целесообразно проводить расслоение партии на одно-родные части для обеспечения отбора представительной выборки.

Формирование выборок продукции для сертификации. Выборки единиц продукции из партии формируются для определения и (или) контроля среднего значения (математического ожидания) измеряемой величины как меры качества изготовления; среднего квадратического отклонения (или дисперсии) измеряемой вели-чины как меры однородности качества изготовления; доли pea-лизаций измеряемой случайной величины, находящейся в задан-ном допуске, и вероятности выполнения контрольных норм при различных методах измерения (пороговом или абсолютном); то-лерантных (допустимых) пределов и т. д. Достоверность оценки качества партии продукции определяется организацией отбора единиц продукции в выборку.

Существует несколько типовых способов отбора единиц про-дукции в выборку: случайный, типический (расслоенный) и направленный (преднамеренный). Случайный отбор заключается в извлечении выборки объема з единиц из партии объема Н, при котором каждой из возможных выборок обеспечивается одина-ковая вероятность отбора. При типическом (расслоенном) отборе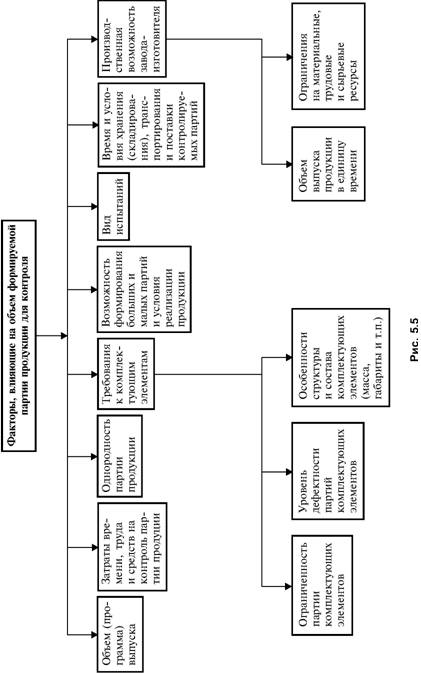

партия продукции сначала подразделяется на качественно однородные (типические) группы (слои) в отношении контролируемого показателя, а затем из каждой группы методами случайного отбора извлекают единицы продукции. Сумма единиц продукции, отобранных пропорционально по группам, равна объему выборки. При направленном отборе из партии объема N извлекается выборка объема n таким образом, чтобы отобранные единицы продукции обладали определенными, наперед заданными свойствами.

«Сырьевая» и «технологическая» однородность партии продукции при анализе, например, механических свойств (твердость, прочность и т. п.) позволяет комплектовать выборку методом направленного отбора «слабейших» изделий партии. Различают три способа представления продукции для контроля: «ряд», «россыпь», «в упаковке».

При способе «ряд» продукция, поступающая для контроля, упорядочена. Ее единицы могут иметь сплошную нумерацию, например 0, 1, 2, … Изделия, отмеченные любым номером, можно легко отыскать и извлечь. Количество единиц продукции, поступающей на контроль, ограничено. При способе «россыпь» единицы продукции, поступающие на контроль, неупорядочены, их невозможно нумеровать и нельзя отыскать и извлечь какую-то определенную единицу; количество единиц, поступающих на контроль, велико. При способе «в упаковке» единицы продукции, поступающие для контроля, не могут быть упорядочены и пронумерованы, так как находятся в контейнерах, ящиках, коробках одного и того же объема. Упаковочные единицы имеют те же особенности, что и продукция, поступающая по способу «ряд».

Случайный отбор с применением случайных чисел используют при проверке продукции, поступающей на контроль по способу «ряд». Для этого N единиц продукции, входящих в партию, нумеруют порядковыми числами от 0 до N – 1. Число N – 1 определяет необходимое число знаков н случайных чисел. Величина н выбирается из условия 10^? ? N – 1. Существующие таблицы случайных чисел содержат k-значные десятичные числа. При ? < k берутся только n знаков каждого числа (слева, справа или посередине), а остальные знаки отбрасывают. Из таблицы случайных чисел выбирают n чисел (n – объем выборки). Порядок их выбора может быть произвольным, при этом числа, большие N – 1, а также повторяющиеся, опускают.

Выборка составляется из единиц продукции, порядковые номера которых соответствуют n отобранным случайным числам.

Многоступенчатый отбор предполагает извлечение из партии сначала укрупненных групп единиц, затем групп, меньших по объему, и так до тех пор, пока не будут отобраны отдельные единицы продукции, которые должны подвергнуться испытаниям. Частным случаем многоступенчатого отбора является двухступенчатый отбор, при котором партия разбивается на группы и производится сначала отбор групп, а затем внутри групп – отбор единиц продукции. На обеих ступенях отбор производится случайным образом. Число ступеней отбора не должно быть большим из-за организационных сложностей формирования выборки. Многоступенчатый отбор отличается от расслоенного тем, что при первом способе отбирают не все группы изделий, а при втором – отбор производится из всех без исключения групп. Многоступенчатый отбор применяют для испытаний продукции в упаковке. Из отобранных упаковочных единиц на первой ступени извлекают отдельные изделия методами случайного отбора (при выборочном контроле) или все изделия (при сплошном контроле), и на основе полученных данных выносят суждение о качестве продукции.

Отбор «вслепую» применяют для продукции, поступающей на контроль по способу «россыпь», а также в том случае, когда применение метода отбора с использованием случайных чисел затруднено или экономически нецелесообразно. Единицы продукции должны отбираться независимо, из разных частей партий. Метод не применяют, когда бракованные изделия можно определить органолептически. Он обеспечивает независимость попадания изделий в выборку, но не гарантирует равную вероятность попадания в выборку единиц продукции.

Систематический (механический) отбор применяют для продукции, если задан определенный порядок следования единиц продукции. Изделия отбирают через фиксированный интервал времени или через определенное число изделий (каждое 10-е, каждое 20-е и т. д.). При этом в следующих одна за другой единицах продукции период изменения контролируемого параметра не должен быть равен периоду отбора изделий. Этот способ обеспечивает равную вероятность попадания каждой единицы продукции в выборку при случайном начале отсчета периода, но не обеспечивает независимость попадания единицы продукции в выборку (в отличие от отбора «вслепую»).

Основные подходы для определения объема выборки. Существуют три подхода определения объема выборки: статистико-вероятно-стный, экономический и комбинированный. При статистико-вероятностном подходе основой процедур вычисления объема n выборки являются соотношения, связывающие объем n выборки с точностью и достоверностью получаемых оценок показателей, или применяется прием «обращения» относительно величины n в статистических критериях проверки гипотез. Экономический подход основан на расчете потерь, обусловленных расходами на проведение испытаний (с учетом разрушения испытываемых изделий) и последствий от принятия того или иного решения по результатам испытаний при некотором объеме n выборки. Комбинированный подход базируется на совместном использовании ста-тистико-вероятностного и экономического подходов.

Рассмотрим наиболее распространенный статистико-вероят-ностный подход определения объема выборки. Исходными данными для вычисления объема выборки являются предельная абсолютная Дч или относительная дч ошибки в оценке среднего значения показателя и предельная абсолютная ошибка Dp в оценке доли признака; степень достоверности оценки, выраженная доверительной вероятностью q.

В табл. 5.6 приведены формулы для расчета объема выборки при случайном и систематическом отборе единиц продукции для оценки среднего значения показателя качества и доли единиц продукции, обладающих определенным признаком (например доля дефектных единиц).

Таблица 5.6

Примечания: 1. Принятые обозначения: ²– ожидаемое значение дисперсии измеряемой величины; V – коэффициент вариации; p – ожидаемое значение доли единиц продукции, обладающих данным признаком; t_q (n 1) – квантиль распределения Стьюдента для доверительной вероятности q и числа степеней свободы n– 1.

2. При расчете n значение округляется до ближайшего целого числа.

В табл. 5.6 учтено, что измеряемая величина имеет нормальное распределение. При больших n (n ? 30) для упрощения расчетов целесообразно вместо значения t_q (n—1) использовать квантиль нормального распределения u_q.

Для больших партий расчет объема выборки без повторения можно проводить по более простым формулам для выборки с повторением.

При случайном многоступенчатом (двухступенчатом) отборе объем выборки определяют: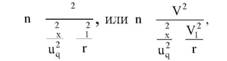

где V₁², V₁ – соответственно межгрупповые дисперсия и коэффициент вариации измеряемой величины; r – число первичных упаковочных единиц, подлежащих отбору, которое зависит от количества первичных упаковочных единиц в партии R:

r………..Все 5 1/20 часть (5 %) 20

R………. 1–5 6 – 99 10 – 399 400 и более.

Предельные объемы выборки при многоступенчатом отборе: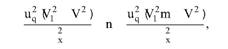

где m – число изделий в упаковочной единице.

Объем выборки при типическом (расслоенном) отборе рассчитывают по следующим формулам:

выборка без повторения выборка с повторением

где V^—2 – среднее частных дисперсий по слоям.

Объем выборок из i-го слоя вычисляется по следующим формулам:

выборка, пропорциональная объему слоев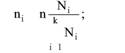

выборка с учетом изменения измеряемой величины в слоях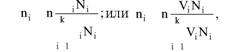

где N_i – объем слоя; k – число слоев в партии; V_i² – ожидаемое значение дисперсии измеряемой величины в i-м слое; V_i – ожидаемое значение коэффициента вариации в i-м слое.

Ниже приведены типовые примеры расчета объема выборки с учетом рассмотренных способов их формирования.

Пример 1. Партия проката (N = 100 листов) представлена на испытания для контроля средней толщины листа с относительной погрешностью ? = 0,1 при доверительной вероятности q = 0,9. Необходимо определить объем выборки, если известно, что коэффициент вариации толщины листа равен 0,2.

Способ представления продукции на испытания – «ряд», поэтому для формирования выборки целесообразно использовать случайный отбор. Так как выборка без повторения, то для расчета объема n выборки необходимо воспользоваться формулой из табл. 5.6, заменив значение t_q (n 1) на u_q:

Таким образом, для обоих типов выборок их объем примерно одинаков.

Пример 2. Партия стержней (N = 20 000 шт.), упакованная в 100 ящиков (упаковочных единиц), представлена на испытания для контроля предела усталости. Необходимо определить объем выборки для испытаний, если ? = 0,1; V = 0,3; V_i = 0,05; q = 0,95.

Определим количество ящиков, подлежащих отбору из партии. Для 100 ? R ? 399 количество отобранных упаковочных единиц r = 100/20 = 5.

Для q = 0,95 по таблице квантилей найдем u_q = 1,64. Тогда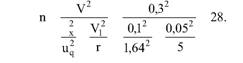

Таким образом, из пяти ящиков, случайно отобранных из партии объемом 100 ящиков, необходимо методом случайного отбора взять 28 стержней (примерно 6 шт. из каждого ящика) на испытания.

Вычислим предельные объемы выборки. Так как N = 20 000, R = = 100, то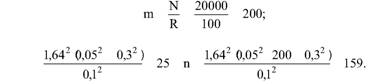

Следовательно, границы объема выборки, исходя из условий примера, составляют 25—159 единиц.

Пример 3. Учитывая условия примера 2, определить объем выборки для испытаний стержней, если вся партия продукции распределена на четыре однородные группы (слоя):

группа 1 – ящики с 1-го по 20-й (R₁ = 20);

группа 2 – ящики с 21-го по 60-й (R₂ = 40);

группа 3 – ящики с 61-го по 80-й (R₃ = 20);

группа 4 – ящики с 81-го по 100-й (R₄ = 20).

Так как партия продукции неоднородна (расслоена), то формирование выборки необходимо проводить методом расслоенного отбора с учетом наличия четырех слоев. Число упаковочных единиц (ящиков) и общий объем выборки определены в примере 2 (r = 5; n = 28).

Определим число упаковочных единиц, которые необходимо отобрать из первого слоя: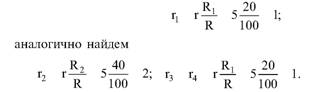

Таким образом, из первого, третьего и четвертого слоев необходимо отобрать по одному ящику, из второго слоя – два ящика.

Определим объем подвыборки, которую необходимо сформировать из продукции первой группы: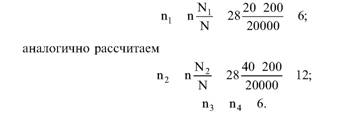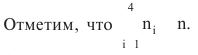

Этот факт обусловлен округлением при вычислении значений n_i.

Рассмотренный пример показывает, что расслоение партии приводит к более сложной процедуре организации формирования выборки при одинаковых требованиях к точности и достоверности.

При сертификации по схеме № 7 (табл. 5.1) часто используется метод параметрического контроля. При параметрическом контроле, в частности надежности, у каждого проверяемого изделия (выборки изделий) определяется один количественный параметр х, который в партии изделий имеет определенное (нормальное, Вейбулла, гамма и т. д.) распределение.

В выборке объема n определяются значения параметра х₁, …, х_п, а также выборочная средняя величина

Оценка партии производится по величине х_ср, для которой (как и для доли дефектных изделий в партии при непараметрическом контроле) устанавливаются два уровня: приемочный х_{ср a} и браковочный х_{ср в}. Соотношение между х_срa и х_срв может быть различным: в случае контроля позитивных показателей х_срa > х_срв, а в случае контроля негативных показателей х_срa < х_срв.

Оценочный норматив (приемочное число) х_срс для среднего значения х_ср контролируемого параметра назначается с учетом следующих условий:

• если х_срa > х_срв, то параметр соответствует установленным требованиям в ТУ при xxcp0 и не соответствует при xxcp0;

• если хсрa < хср в, то параметр хср соответствует установленным требованиям в ТУ при xxcp0 и не соответствует при x x_cp0.

В свою очередь параметрический статистический контроль может быть одноступенчатым или многоступенчатым.

Одноступенчатый контроль осуществляется по результатам одной выборки, а многоступенчатый – по результатам нескольких выборок. При этом каждой выборке в общем случае соответствует свой оценочный норматив (приемочный и браковочный уровень).

Многоступенчатые правила контроля более экономичны по сравнению с одноступенчатыми, но организация их вызывает большие трудности.

Параметрический одноступенчатый контроль. Такой контроль показателей безотказности – наработки до отказа (на отказ, между отказами) – осуществляется по выборочному среднему (5.4) значению T в соответствии со следующими условиями: приемки (соответствия контролируемого показателя заданным требованиям) TT_c; браковки (несоответствия контролируемого показателя заданным требованиям) T Т₀, где Т0 – оценочный норматив выборочного среднего значения наработки до отказа (на отказ, между отказами). В соответствии с этим риски поставщика и заказчика соответственно равны: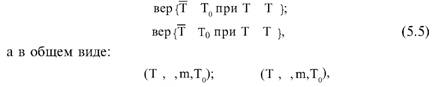

где T_a, T_в – уровни среднего значения наработки на отказ (до отказа, между отказами) соответственно приемочный и браковочный; v – коэффициент вариации наработки на отказ (до отказа, между отказами); m – необходимое для контроля среднего значения наработки на отказ (до отказа, между отказами) количество измерений или отказов.

План контроля (количество измерений m и оценочный норматив Т₀) определяется путем решения уравнений (5.5) относительно m и Т₀.

При нормальном распределении наработки до отказа (на отказ, между отказами) соотношения (5.5) принимают вид: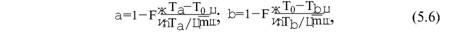

где F (·) – нормированная и центрированная функция нормального распределения.

С учетом зависимостей (5.6) требуемое количество измерений: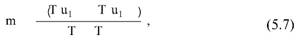

где U_р – квантиль нормального распределения, отвечающая вероятности р (табл. 5.7).

При a = в = ц соотношение (5.7) можно представить в виде: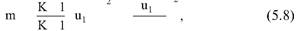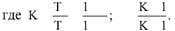

Таблица 5.7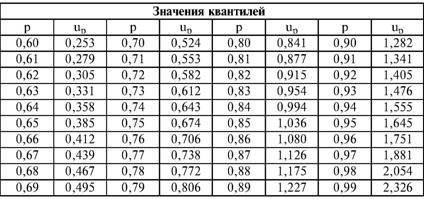

На основании зависимостей (5.6) получаются выражения для оценочного норматива: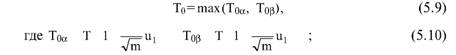

при этом m определяется из соотношений (5.7) и (5.8).

Наконец, требуемый объем (суммарная наработка в процессе испытаний):

t = mT₀ (5.11)

где m и T₀ – величины, рассчитываемые по (5.7) – (5.10).

При распределении наработки до отказа (на отказ, между отказами) по закону Вейбулла соотношения (5.5) принимают вид: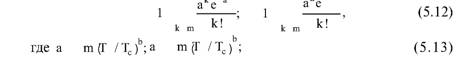

в – параметр формы распределений Вейбулла, однозначно определяющий коэффициент вариации.

Используя соотношения (5.12), (5.13), получим (табл. 5.8):

В результате решения соотношения (5.14) относительно m (см. табл. 5.8) устанавливается необходимое для контроля Ф количество измерений наработки до отказа (на отказ, между отказами):

m = f(T_a, T_в, ?, ?, b). (5.15)

Таблица 5.8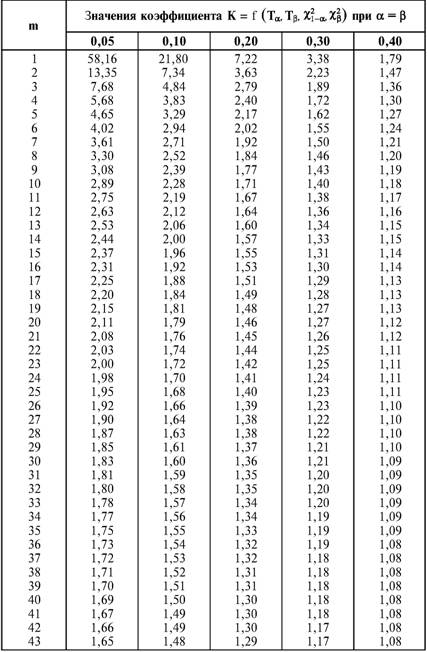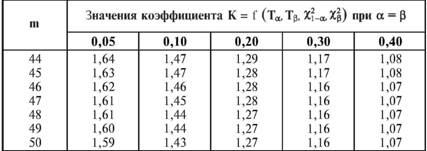

Используя зависимости (5.12), (5.13), получим выражения для оценочного норматива: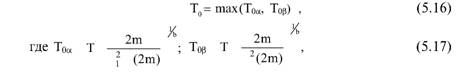

m определяется соотношениями (5.14), (5.15).

Требуемый объем (суммарная наработка в процессе испытаний), как и в случае нормального распределения, определяется выражением (5.11).

Пример 4. Известно, что наработка изделия между отказами имеет нормальное распределение с коэффициентом вариации n = 0,25. В технических условиях (ТУ) на производство изделия установлены приемочный Т_а = 150 ч и браковочный Т_в = 100 ч уровни средней наработки между отказами, а также соответствующие им риски ? = 0,2 и в = 0,1. Требуется установить план одноступенчатого статистического контроля наработки изделия между отказами.

Для ? = 0,2, ? = 0,1 в табл. 5.7 найдем u_1-? = 0,841 и u_1-?= 1,282. По (5.7) определим необходимое для контроля количество измерений: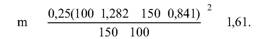

Следовательно, m = 2.

Используя зависимости (5.10), найдем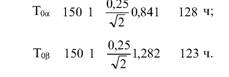

Из соотношения (5.9) определим оценочный норматив Т₀ = 128 ч. С помощью (5.11) найдем требуемую суммарную наработку изделия в процессе испытаний: t = 2256 = 128? ч.

Таким образом, план одноступенчатого статистического контроля наработки изделия между отказами (на отказ) характеризуется величинами t = 256 ч и Т₀ = 128 ч.

Цель статистического анализа безопасности при сертификации – оценка полноты выявления основных источников аварий и достаточности средств и мероприятий для достижения приемлемого уровня безопасности.

Общая схема статистического анализа безопасности представлена на рис. 5.6 и включает:

• составление перечня исходных событий аварии;

• разработку деревьев событий, позволяющих рассмотреть варианты развития аварии от исходного события аварии;

• анализ надежности элементов объекта, позволяющий оценить вероятность наступления конечных состояний;

• анализ последствий развития аварийных процессов (последствия конечных состояний);

• количественный анализ последствий конечных состояний;

• оценка рисков.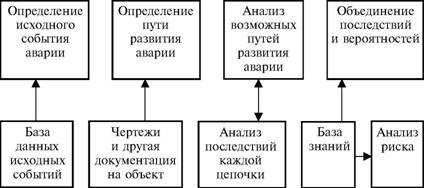

Рис. 5.6

Для достижения цели, сформулированной выше, при проверке решаются следующие задачи: экспертиза данных о надежности;

• оценка полноты исходных событий аварии;

• экспертиза моделирования деревьев событий. При экспертизе данных о надежности оценивают:

• источники получения информации;

• обоснованность выбора элементов каждого типа;

• численные значения показателей надежности;

• последствия отказа;

• соответствие критериев отказа, приведенных в исходных данных, нормативным признакам.

Оценка полноты исходных событий аварии сводится к обоснованию их выбора и оценке их частоты, с тем чтобы анализу были подвергнуты наиболее часто встречающиеся.

При экспертизе деревьев событий необходимо оценить:

• методологию моделирования деревьев событий;

• хронологию развития отдельных событий;

• адекватность моделей деревьев событий критериям отказов. Метод дерева событий дает возможность:

• определить сценарии аварий с различными последствиями;

• определить взаимосвязь отказов элементов с последствиями аварии;

• сократить первоначальный набор потенциальных аварий и ограничить его лишь логически значимыми авариями.

Структура возможного дерева событий представлена на рис. 5.7, где ИСА – исходное событие аварии; А, В, Д – элементы, влияющие на развитие аварийной последовательности; ОА, ОВ, Од – отказ элемента А, В, Д соответственно; КОС – классы определяемых конечных состояний; Т_КОС – время достижения соответствующего конечного состояния; РКОС – вероятность реализации аварийной цепочки; 1_ИСА – интенсивность возникновения исходного события аварии; № – номер цепочки.

Для цепочек развития аварии из исходного события вероятности их реализации равны:

P1 = Ра · Рв · Рд; Р2 = Ра(1 – Рв); Рз=Ра(1—Рв) (1—Рс);

Р4 = 1 – Ра,

где Ра, Рв, Рд – вероятности безотказной работы элементов А, В, Д соответственно.

В результате расчета можно:

• выбрать цепочки с максимальными значениями;

• внутри цепочек выделить наиболее критичные элементы, для которых вероятности отказа максимальны;

• сравнивать между собой вероятности реализации тех или иных сценариев развития аварий.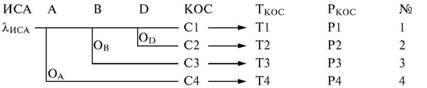

Рис. 5.7

В рамках проверки системы качества целесообразно оценить достаточность мероприятий по поддержанию требуемого уровня безопасности. С этой целью может быть вычислен риск производства как сумма всех рисков индивидуальных сценариев аварий: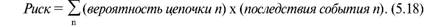

Таким образом, в ходе проверки может быть оценена результативность мероприятий по преодолению последствий наступления исходного события аварии и проведен анализ мер:

• по снижению частот наступления исходных событий аварии (1иса на рис. 5.7);

• по повышению вероятностей безотказной работы элементов, включенных в цепочки развития аварии (P_A, Р_в, Р_д на рис. 5.7);

• по снижению последствий аварий (колонка КОС на рис. 5.7). При анализе безопасности с использованием методологии

дерева событий можно учесть действия персонала (ошибки и корректирующие действия) путем включения их в соответствующие цепочки. Кроме того, при построении цепочек можно учесть наступление различных внешних событий, влияющих на развитие аварийного процесса (например отключение воды при пожаре, обесточение).

Для упрощения анализа безопасности целесообразно использовать методологию FMECA (Failure mode Effects and Criticality Analysis) в табличной форме, т. е. анализ видов, последствий и критичности отказов. Под критичностью отказа здесь понимается совокупность признаков, характеризующих последствия отказа (например по уровню прямых и косвенных потерь, трудоемкости восстановления работоспособного состояния и т. п.) оборудования. Применение методологии FMECA в табличной форме регламентируется международным стандартом МЭК 812, национальными стандартами ряда развитых стран (США, Японии, Германии), фирменными стандартами (Форд, Фольксваген, Тоёта и др.).

Документация, относящаяся к FMECA и содержащая, например, перечни критических отказов и критических технологических процессов, является хорошим индикатором наличия элементов системы качества, обеспечивающих безопасность.

Задача лица, проводящего проверку аспектов обеспечения безопасности, оценить полноту анализа видов, последствий и критичности отказов оборудования (если методология БМЕСА использовалась на предприятии). В противном случае эксперт-аудитор имеет возможность сам провести анализ критичности оборудования или технологических процессов (операций), воспользовавшись БМЕСА-анализом на основе специально разработанных таблиц.

В общем случае целесообразно применять три таблицы. Первая содержит балльные оценки частоты отказов оборудования (нарушений технологического процесса); вторая – балльные оценки возможности выявления (диагностирования) отказа или нарушения; третья – балльные оценки последствий отказа. Пример таких шкал оценок приведен в табл. 5.9.

Таблица 5.9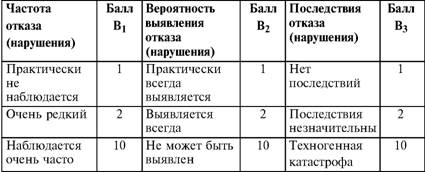

Критичность i-го отказа (нарушения) вычисляется по формуле:

С_i = B_1i?B_2i?B_3i, (5.19)

где B_1i, B_2i, B_3i – балл, выставленный экспертом по факторам «частота отказа», «вероятность выявления отказа», «последствие отказа» соответственно.

Если значение q превышает некоторый критический уровень Скр (например, Скр = 125), то такой отказ или нарушение технологического процесса признаются критически (с точки зрения безопасности).

Составив перечень критических нарушений, эксперт имеет возможность провести целенаправленную проверку мероприятий, препятствующих нарушениям (отказам).

Во многих случаях полезно строить диаграммы Парето в аспекте рисков различных нарушений, вычисленных по формуле (5.18), или критичностей, вычисленных по формуле (5.19). Применение диаграммы Парето в этой ситуации дает возможность выделить наиболее значимые (критические) нарушения, для которых оценивается система мероприятий, блокирующих их.

1. Поясните цель использования статистических методов на предприятии.

2. Охарактеризуйте область использования статистических методов.

3. Какие статистические методы рекомендуют использовать стандарты ИСО серии 9000?

4. Перечислите основные этапы построения диаграммы «причины – результат».

5. Приведите пример использования диаграммы «причины – результат».

6. В чем состоит цель построения диаграммы Парето?

7. Какие задачи позволяет решить корреляционный анализ?

8. Для чего необходима оценка точности и стабильности производственных процессов?

9. Как определить достаточность мероприятий по безопасности? 10. Что такое критичность отказа?

1. Шиндовский Э., Щюрц О. Статистические методы управления качеством. Контрольные карты и планы контроля / Пер. с нем. – М.: Мир, 1976.

2. Куме X. Статистические методы повышения качества / Пер. с англ. – М.: Финансы и статистика, 1990.

3. Лапидус В. А. О концепции развития, внедрения и стандартизации статистических методов управления качеством продукции в СССР // Надежность и контроль качества. 1991. № 2, 4, 6.

4. Кейн В. Э. Индексы воспроизводимости процессов // Курс на качество. – 1993.

5. Аронов И.З., Александровская Л.Н. Прудникова Е.А. Анализ надежности при сертификации систем качества // Приборы и системы управления. – 1992. № 7.

6. Бирюкова З. Ф., Букринский А. М., Грозовский Г. И. и др. Применение вероятностного анализа безопасности к оценке текущего уровня безопасности атомной станции.

7. Proceeding of an International Symposium on the Use of Probabilistic Safety Assessment for Operational Safety. Spa 91, IAEA, 1991.

8. Швыряев Ю. В. Вероятностный анализ безопасности атомных станций. Методика выполнения. – М.: ИАЭ им. И. В. Курчатова, 1992.

9. Шпер В. Л. Семь простых методов контроля качества / Надежность и контроль качества. – 1992. № 19.

10. Харингтон Дж. Х. Управление качеством в американских корпорациях / Пер. с англ. – М.: Экономика, 1990.

11. Кокс Д., Хинкли Д. Теоретическая статистика. – М.: Мир, 1978.

12. Большев Л. Н., Смирнов Н. В. Таблицы математической статистики. – М.: Наука, 1983.

13. Аронов И. 3., Шоничев Г. В. Методы формирования партий и выборок для контроля качества продукции. Надежность и эффективность в технике: Справочник. Т. 7. Качество и надежность в производстве. – М.: Машиностроение, 1989.