• Главная
• Контакты
• Нашёл ошибку
• Прислать материал
• Добавить в избранное

Помимо классического метода наименьших квадратов для определения неизвестных параметров линейной модели множественной регрессии ?0…?m используется метод оценки данных параметров через ?-коэффициенты (коэффициенты модели регрессии в стандартных масштабах).

Построение модели множественной регрессии в стандартизированном или нормированном масштабе означает, что все переменные, включенные в модель регрессии, стандартизируются с помощью специальных формул.

Посредством процесса стандартизации точкой отсчёта для каждой нормированной переменной устанавливается её среднее значение по выборочной совокупности. При этом в качестве единицы измерения стандартизированной переменной принимается её среднеквадратическое отклонение ?.

Факторная переменная х переводится в стандартизированный масштаб по формуле: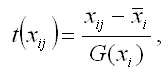

где xij – значение переменной xjв i-том наблюдении;

G(xj) – среднеквадратическое отклонение факторной переменной xi;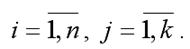

Результативная переменная у переводится в стандартизированный масштаб по формуле: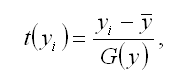

где G(y) – среднеквадратическое отклонение результативной переменной у.

Если между исследуемыми переменными в исходном масштабе является линейной, то процесс стандартизации не нарушает этой связи, поэтому стандартизированные переменные будут связаны между собой линейно: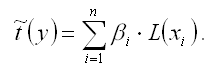

Неизвестные коэффициенты данной функции можно определить с помощью классического метода наименьших квадратов для линейной модели множественной регрессии. В этом случае минимизируется функционал F вида: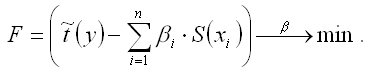

В результате минимизации данного функционала получим систему нормальных уравнений, переменными в которой будут являться парные коэффициенты корреляции между факторными и результативной переменной. Такой подход основывается на следующем равенстве: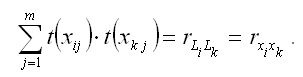

Система нормальных уравнений для стандартизированной модели множественной регрессии имеет вид: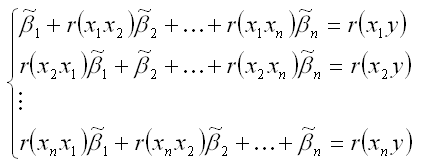

В связи с тем, что полученная система нормальных уравнений является квадратной (количество уравнений равняется количеству неизвестных переменных), то оценки коэффициентов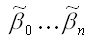

можно рассчитать с помощью метода Крамера, метода Гаусса или метода обратных матриц.

Рассчитанные из системы нормальных уравнений ?-коэффициенты в стандартизированном масштабе необходимо перевести в масштаб исходных данных по формулам: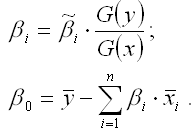

Рассмотрим метод Гаусса решения квадратных систем линейных уравнений. Суть данного метода заключается в том, что исходная квадратная система из n линейных уравнений с n неизвестными переменными преобразовывают к треугольному виду. Для этого в одном и уавнений системы оставляют все неизвестные переменные. В другом уравнении сокращают одну из неизвестных переменных для того, чтобы число неизвестных стало (n-1). В следующем уравнении сокращают две неизвестных переменных, чтобы число переменных стало (n-2). В результате данных преобразований исходная система уравнений примет треугольный вид, первое уравнение которой содержит все неизвестные, а последнее – только одну. В последнем уравнении системы остаётся (n-(n-1)) неизвестных переменных, т. е. одна неизвестная переменная, которая называется базисной. Дальнейшее решение сводится к выражению свободных (n-1) неизвестных переменных через базисную переменную и получению общего решения квадратной системы линейных уравнений.